거듭제곱은 같은 수 또는 문자를 여러번 곱하는 것을 거듭제곱이라고 합니다.
수식 y = x를 코드로 구현
파이썬에서 거듭제곱은 **으로 구현합니다
%matplotlib inline # %matplotlib inline 은 주피터 브라우저에서 그림을 곧바로 볼 수 있도록
# 내부에 그리게 해주는 코드 입니다.
import numpy as np
import matplotlib.pyplot as plt
def my_func(x):
a = int(input())
return x ** a
x = np.linspace(0,2)
y = my_func(x)
plt.plot(x, y)
plt.xlabel("x",size=14)
plt.ylabel("y",size=14)
plt.grid()
plt.show()
%matplotlib inline 라는 코드가 가장 첫 줄에 있는데, 이것은 주피터 브라우저 내부에서 곧바로 그림을 볼 수 있도록
inline(내부에) 그림을 바로 그리도록 하는 코드 입니다.

파이썬에서 제곱근은 값에 1/2 를 제곱해서 표현하는데, 이를 **0.5 로 수식해서 표현할 수 있습니다.
우선 파이썬 기본 함수로 작성해볼게요.
import numpy as np
import matplotlib.pyplot as plt
def my_func(x):
return x ** 0.5 + 1
x= np.linspace(0,9)
y= my_func(x)
plt.plot(x,y)
plt.xlabel("x",size=12)
plt.ylabel("y",size=12)
plt.grid()
plt.show()

** 0.5 를 하지 않아도 Numpy 에서는 제곱근을 구현할 수 있는 기능을 제공합니다.
바로 squr() 함수인데요.
square root 의 약자로 스퀘어 루트 라고 읽거나 알파벳 약자대로 읽기도 합니다.
.squr(x) = √x
import numpy as np
import matplotlib.pyplot as plt
def my_func(x):
return np.sqrt(x) + 1 # 제곱근 함수 사용 sqrt
x= np.linspace(0,9)
y= my_func(x)
plt.plot(x,y)
plt.xlabel("x",size=12)
plt.ylabel("y",size=12)
plt.grid()
plt.show()
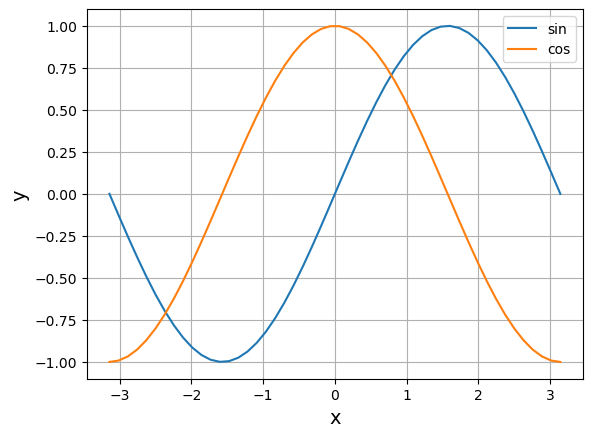
삼각함수의 값 또한 Numpy 로 그래프를 구현할 수 있습니다.
sin, cos, tan의 값을 구하는 공식에 따라 그래프를 구현합니다.

%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
def my_sin(x):
return np.sin(x) # sin(x)
def my_cos(x):
return np.cos(x) # cos(x)
x = np.linspace(-np.pi, np.pi) # -파이부터 파이(라디안)까지
y_sin = my_sin(x)
y_cos = my_cos(x)
plt.plot(x, y_sin, label="sin")
plt.plot(x, y_cos, label="cos")
plt.legend()
plt.xlabel("x", size = 14)
plt.ylabel("y", size = 14)
plt.grid()
plt.show()
import random
random.randrange(1,7)
랜덤 뽑기의 경우 파이썬의 random 모듈로 이전에 사용해본 적 있습니다.
이번에는 numpy의 random 기능을 사용해봤어요.
import numpy as np
r_int = np.random.randint(7) // 0에서 7까지의 랜덤한 수
print(r_int)
둘 다 한 개의 랜덤의 수를 출력합니다.

랜덤이 균일하게 분포된 균일한 난수의 경우 정규분포 그래프로 표현이 가능합니다.
이것을 파이썬으로 구현하면 아래와 같습니다.
균일한 난수 (정규분포 그래프)
%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
n = 1000
x = np.random.rand(n) @ 0~1의 균일한 난수
y = np.random.rand(n) @ 0~1의 균일한 난수
plt.scatter(x, y) # 산포도 플롯
plt.grid()
plt.show()
import numpy as np
import matplotlib.pyplot as plt
n = 1000 # 샘플의 수
x = np.random.randn(n) # 정규 분포를 따른 난수의 분포
y = np.random.randn(n) # 정규 분포를 따른 난수의 분포
plt.scatter(x,y) # 산포도 플롯
plt.grid()
plt.show()
절댓값은 값과 0 사이의 거리를 나타냅니다. (음수에서 마이너스를 뗀 양수의 값처럼요.)
인공지능에서 0(제로)를 중심으로 한 값의 퍼짐 상태를 확인하기 위해 주로 사용합니다.
절댓값은 양과 음을 무시하고 얻을 수 있는 음이 아닌 값을 말합니다.
음수의 값에서는 그 부호를 빼면 절댓값이 됩니다.
절댓값은 Numpy 의 abs() 함수를 사용합니다. absolute의 약자.
이것은 파이썬의 기본함수에도 있는 기능인데
a = -5
abs(a) # 파이썬 기본 함수5
이렇게 사용할 수도 있고, numpy를 활용해서
import numpy as np
x = [-5, 5, -1.25, np.sqrt(5), -np.pi/2] # 여러값을 리스트에 저장한 후
print(np.abs(x)) # 절대값을 구한다[5. 5. 1.25 2.23606798 1.57079633]numpy abs() 는 이렇게 리스트에 여러가지 값을 저장한 후 절대값을 구하는 방법으로도 사용할 수 있습니다.
이 함수를 활용해서 절댓값의 이미지를 구할 수 있습니다.
절댓값을 이용해서 양과 음의 여부에 관계없이 0으로 부터 떨어진 정도를 파악할 수 있습니다.
sin()과 cos()의 절댓값을 구해볼게요.
%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
x = np.linspace(-np.pi, np.pi) # -파이부터 라디안까지
y_sin = np.abs(np.sin(x)) # sin()함수의 절댓값을 취한다.
y_cos = np.abs(np.cos(x)) # cos()함수의 절댓값을 취한다.
plt.scatter(x, y_sin, label = "sin")
plt.scatter(x, y_cos, label = "cos")
plt.legend()
plt.xlabel("x", size=14)
plt.ylabel("y", size=14)
plt.grid()
plt.show()
이렇게 하면 음수를 제외하고 0 까지의 분포도를 확인할 수 있습니다.
인공지능 수학은 이후에 실전에서 조금 더 활용해서 예제들을 올리는 것으로 할게요.
'AI 머신러닝 딥러닝 > AI 수학 입문 공부일지' 카테고리의 다른 글
| AI 인공지능 수학 공부일지 7. 스칼라scalar, 벡터vector, 행렬matrix 텐서tensor (1) | 2023.01.04 |
|---|---|
| AI 인공지능 수학 공부일지 5. matplotlib 기초 (0) | 2022.10.21 |
| AI 인공지능 수학 공부일지 4. Numpy 기초 행열 (0) | 2022.10.21 |
| AI 인공지능 수학 공부일지 3. 판다스 pandas 모듈 (0) | 2022.10.21 |
| AI 인공지능 수학 공부일지 2. BeautifulSoup로 네이버 금융 코스피 지수 추출하기 (0) | 2022.10.21 |